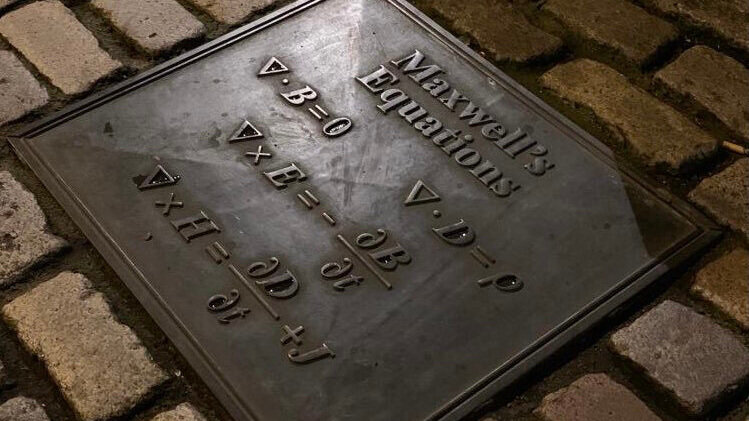An Introduction to Maxwell and his Equations
At the foot of Maxwell’s statue, George Street, Edinburgh
Who was Maxwell and what is the historical significance of his equations?
In the mid-nineteenth century Scottish mathematical physicist James Clerk Maxwell (1831-1879) synthesized the experimental knowledge of electricity and magnetism into a concise set of equations. That changed the world. Without him the socioeconomic progress humans derive from the use of technology empowered by electricity, would be almost unimaginable, and you wouldn’t be reading this article.
Maxwell's theory represented the first Classical theory of a field of vectors. This was followed by other theories and types of interactions to explain other fields. Indeed, Maxwell’s significance can hardly be overstated, standing on the shoulders of Newton, his work was only the second great unification of physics. Maxwell’s legacy directly effects almost every human that has lived since. Massive growth in energy consumption per capita has led a revolution in most measures of welfare, including life expectancy, poverty reduction, technology adoption, female education, dissemination of ideas and those living in democracy.
Maxwell described the existence of electromagnetic wave as propagating in a vacuum at the speed of light. The speed of light had already been measured. Maxwell understood light as the high frequency manifestation of the same phenomena that governs the mutual influence of the electrical charges at rest (static), in motion (electric currents), and the relationship between electric currents and magnetism. Maxwell’s primary subject of study came to be considered a distinct domain. Prior to Maxwell, electricity and magnetism had been understood separately. In his highly influential work Electricity and Magnetism (1873) Maxwell first published the equations that now bear his name. They created the theoretical foundations for the study and application of electromagnetism.
Maxwell's equations are relativistic invariant and confirm what Einstein formulated In 1905 In his theory of relativity. Einstein was attempting another great unification of physics. Today, we continue trying to establish a single unified field theory.
Who was Michael Faraday and what is the connection to Maxwell’s third equation?
Electricity and magnetism emerged as a self-contained science in the 19th century. Michael Faraday (1791-1867) made an essential contribution by discovering the law of electromagnetic induction. An experimental figure of unrivalled stature, among other things Faraday provided for the existence of the electromagnetic field - the state of the matter through which electrical and magnetic interactions are transmitted. He also discovered the laws of electrolysis, foreseeing the existence of the elementary electric charge.
Faraday’s experiments were largely based on his intuitive forecasts. Maxwell's theory was quickly and broadly accepted as a fundamental leap in human understanding of physical reality. In Maxwell's theory, the electromagnetic field appears as a mediator of the transmission of electromagnetic interactions between physical objects. This understanding overturned the older theory of Distance Action introduced by Isaac Newton.
What are the equations and what do they mean?
Maxwell's equations describe the Classical Theory of electromagnetic phenomena. The four equations cover the dynamic and static behaviour, or characteristics, of both electric and magnetic fields.
The physical contents of these equations are the results of eight fundamental experiments conducted in total isolation. For the behaviour of the fields in substance there is another experiment (Gauss's Law in Substance, also discovered by Michael Faraday).
First Equation: Gauss's law - The Law of Electric Flux. A static state law (static in time)
Second Equation: Gauss's law for magnetism - The Law of Magnetic Flux. This is also a static state law (static in time)
Third Equation: Faraday's law - The Law of Electromagnetic Induction. A dynamic evolutionary law (evolution in time)
Fourth Equation: Ampère's law (with Maxwell's addition) - The Law of magnetic circuits. This is also a dynamic evolutionary law (evolution in time).
The local forms of the laws of the electromagnetic field in immobile environments make up a system of 4 partial and first order linear differential equations, known as Maxwell's equations. A seven-equations system is obtained (4 + 3 = 7 equations) if we describe relationships in matter, in linear, and in isotropic environments. Those 7 equations uniquely determine the electromagnetic field under the referenced conditions. From a mathematical point of view, Maxwell’s system of laws describing the electromagnetic field is complete and non-contradictory.
Since none of the laws of electromagnetism can be determined from the others, it follows that the system of laws has an independent character. All electromagnetic phenomena encountered in electrical engineering can be explained and mathematically modelled using Maxwell’s system of equations, as for all practical purposes Maxwell’s system is physically complete.
How does Maxwell’s 3rd equation relate to new innovation?
We seek the twin objectives of growth in socioeconomic welfare and decarbonisation of society as essential preconditions for a sustainable future. There are those that suggest this is not possible. Certainly, the data on energy consumption and measured human welfare strongly suggests we are unlikely to achieve that goal without very significant further electrification of economies globally.
The vast majority of the world’s electricity reaches consumers through Alternating Current (AC) systems. Maxwell’s Third Equation: Faraday’s law of Induction is essential to all AC systems. We empower our dreams and ambitions through technology that utilises that electric wave. The cleanliness of that AC wave’s form is critical to its stability and value.
Historically, large carbon emitting power stations have been the primary providers of that AC wave. Over the last 130 years, engineers have become very good at maintaining that wave within the very narrow +/- 1% parameters to ensure our electricity supply. The problem is we can no longer afford the carbon emissions, and we don’t have an affordable solution to keeping the system stable without those power stations. Solar and wind do not provide their carbon free electricity in the same way. They actually make the system less stable. Many proposed solutions for system stability are economically unaffordable at scale, and the race is on to find a solution.